Abstract

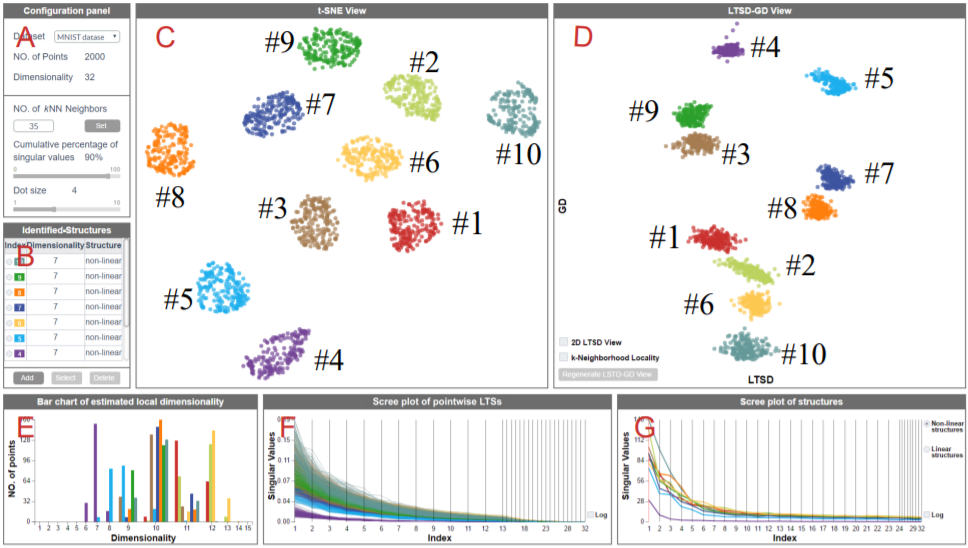
Many approaches for analyzing a high-dimensional dataset assume that the dataset contains specific structures, e.g., clusters in linear subspaces or non-linear manifolds. This yields a trial-and-error process to verify the appropriate model and parameters. This paper contributes an exploratory interface that supports visual identification of low-dimensional structures in a high-dimensional dataset, and facilitates the optimized selection of data models and configurations. Our key idea is to abstract a set of global and local feature descriptors from the neighborhood graph-based representation of the latent low-dimensional structure, such as pairwise geodesic distance (GD) among points and pairwise local tangent space divergence (LTSD) among pointwise local tangent spaces (LTS). We propose a new LTSD-GD view, which is constructed by mapping LTSD and GD to the x axis and y axis using 1D multidimensional scaling, respectively. Unlike traditional dimensionality reduction methods that preserve various kinds of distances among points, the LTSD-GD view presents the distribution of pointwise LTS (x axis) and the variation of LTS in structures (the combination of x axis and y axis). We design and implement a suite of visual tools for navigating and reasoning about intrinsic structures of a high-dimensional dataset. Three case studies verify the effectiveness of our approach.