作者:Yong Wang, Zhihua Jin, Qianwen Wang, Weiwei Cui, Tengfei Ma and Huamin Qu
本文发表于 VIS2019, 来自于香港科技大学的可视化小组(屈华民教授领导)的研究
1. 简介
图数据广泛用于各个领域,例如生物信息学,金融和社交网络分析。在过去的五十年中,已经提出了许多图布局算法,来满足所需的视觉要求,例如更少的边缘交叉,更少的节点遮挡以及更好的聚团保护。传统的图布局算法大致可以分为两个方向:基于弹簧,能量模型和基于降维模型。当用户使用特定的图布局时,取得好的可视化效果往往需要许多参数的实验,对于没有相关经验的用户来说,是一个不小的挑战。由于特定于算法的参数和布局效果通常取决于输入的图结构,因此我们考虑是否可以使用深度学习来学习别人的布局算法。
这个问题有以下三个挑战:
- 模型选择: 图布局算法不同与普通的分类问题,它的输入是复杂的图结构,输出是点的坐标(不定长二维数组)。
- 损失函数设计: 图布局的结果很难判断好坏(很多时候是主观的印象),除此之外,图布局通过旋转和放缩之后,依然具有相同的结构。
- 训练数据的缺少:不同于图像领域有 Imagenet, MNIST 等数据集,图布局算法并没有这方面的数据集
本文提出一种基于 graph-LSTM 的方法来直接根据输入图的拓扑结构生成图布局结果。本文使用广度优先搜索(BFS)将图拓扑信息转换为一系列邻接矩阵,其中每个子向量对序列中每个节点及其相邻节点之间的连接信息进行编码。还提出了一种基于 Prostats Statistics 的损失函数,该函数对于图的平移,旋转和缩放基本上是不变的,以此评估学习质量并指导模型训练。在训练过程中,使用了三种图数据集(网格图,星形图和随机图)。
2. 相关工作
- 传统的图布局算法大致可以分为两个方向:基于弹簧,能量模型和基于降维模型。基于弹簧,能量模型最著名的有力引导模型,ForceAtlas 等。基于降维有 PivotMDS 以及 tsNET 等算法。除此之外还有一些基于层次布局和空间索引树的优化,比如 FM3 算法。
- 图神经网络被用于各种图相关学习的研究,过去基于谱(Spectral)卷积的算法往往只能用于固定结构的图数据研究,除了谱卷积之外,非谱方法还可以直接在图上进行卷积,此类算法将节点的邻域定义为传入范围,并且提出了各种方法,例如 Semi-Supervised Classification with Graph Convolutional Networks 等。他们大多应用于点预测,边预测,与本文的任务还是有所区别。
- 已有一些研究将深度学习,机器学习应用到图布局当中,比如 Kwon et al.(VIS 2017)提出了一种机器学习方法,为用户提供了图布局的快速预览,并使用了图的拓扑结构信息来计算不同图结构之间的相似度。H. Haleem et al.提出了基于神经网络的方法来评估图布局绘制结果。
3. 算法与模型
问题定义
图布局算法的输入是$G=(V,E) \quad V={v{1},v{2}…v{n}} \quad E\subseteq V \times V $,输出是$C = {c{v}|v ∈ V}$, 其中$c_v$属于二维向量。
传统的图布局算法考虑不同的评价标准来设计算法,在本文中,我们将图布局算法转化为学习问题,一旦成功训练了深度学习模型,当给定一个新图数据,它就可以自动分析图结构并直接生成一个带有训练数据特性的布局效果。

模型设计
- 由于图布局的输出是一个不定长的二维数组,cv 领域常用的 CNN 网络并不适用于此类问题,第一 CNN 网络无法处理图数据的输入,其次 CNN 网络的输出一般是一个定长的数组。
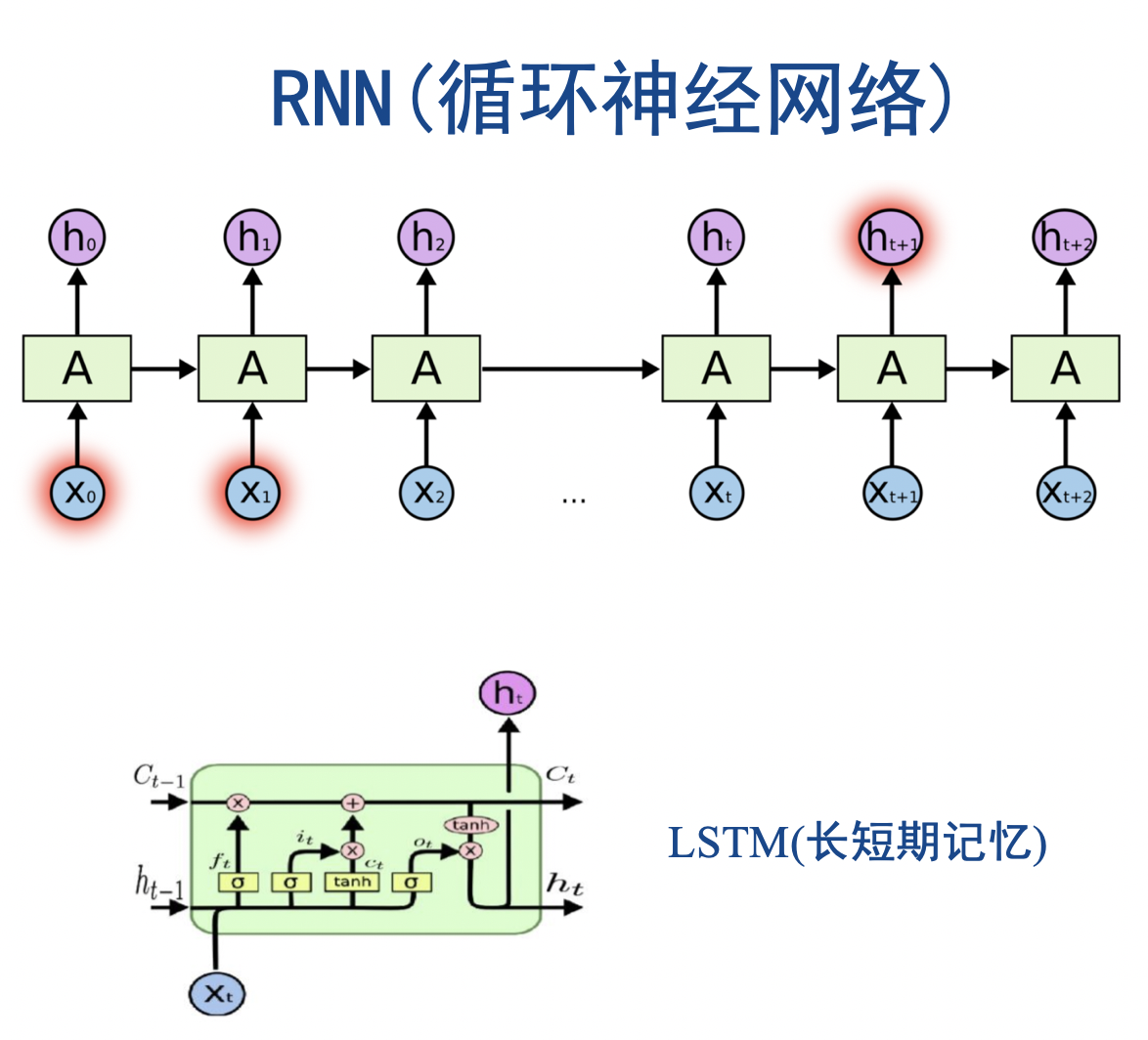
- 本文使用 LSTM(长短期记忆)作为基础模型,LSTM 是 RNN(循环神经网络)的变种,一开始用于自然语言处理方向。 他可以同时参考过去网络中的最新信息以及较久的信息。我们可以使用点的特征序列作为输入向量,顺序输出每个点的二维坐标。LSTM 的结构和公式如下图所示, $c{t-1}, h{t-1}, x{t}$是他的输入,$h{t}, c_{t}$是他的输出。
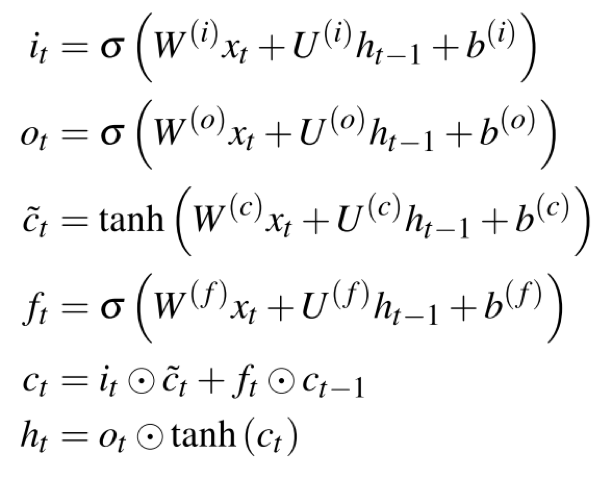
- 但是这样的方案并没有考虑到图中边的信息,所以参考 skip-connection 的技术,可以对于 LSTM 网络进行改进,将边作为两个神经元之间的联系,如下图所示,其中$P(t)$表示该点的领域, 和标准 LSTM 的主要区别在于,本文的模型进一步考虑了图中边的信息。除此之外本文还使用了双向 LSTM 的技术,使其能更全面考虑所有点对某个点的贡献。
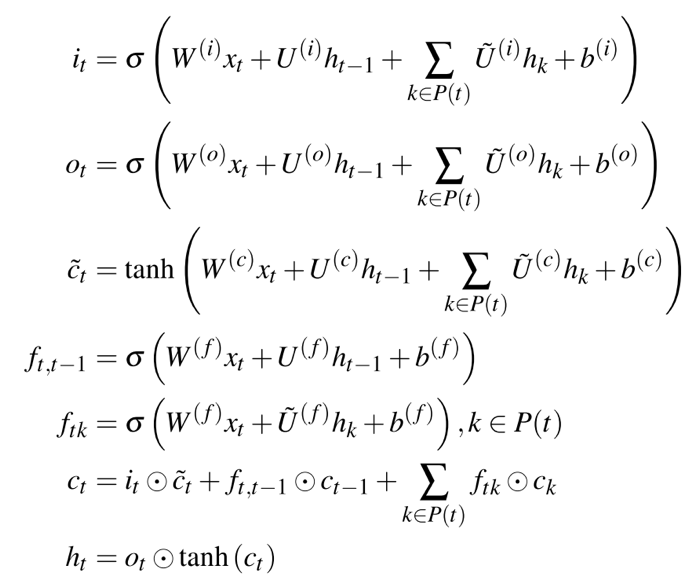
- 所以本文的模型如下所示。输入点的顺序是图的 BFS(广度优先搜索)序列,每个节点都由一个邻接向量表示,该向量编码了与先前节点的连接情况。 黄色的虚线箭头传播了先前节点对后续节点图形的总体影响,而弯曲的绿色箭头(图的边)反映了实际的图结构,为了生成最终的 2D 节点布局,还考虑前后的信息(双向 LSTM)。
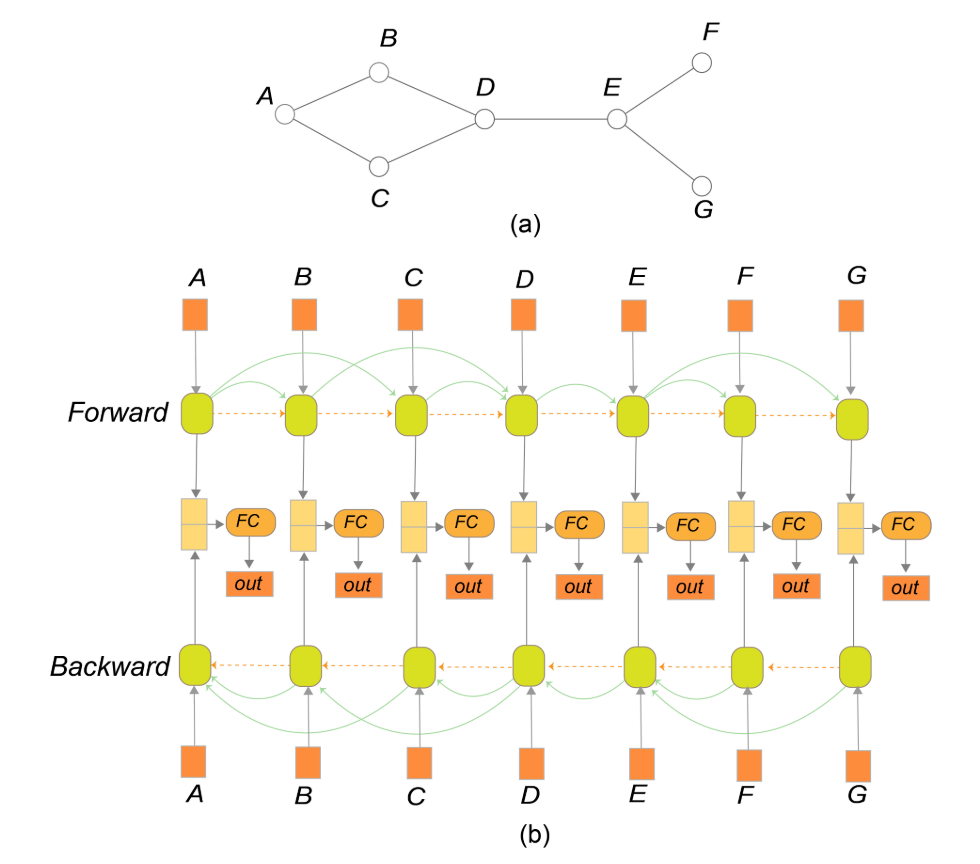
- 本文还对于 loss function 进行了重新的设计, 考虑了旋转,放缩不变性等原理。基于 Prostats Statistics 提出了一种损失函数。
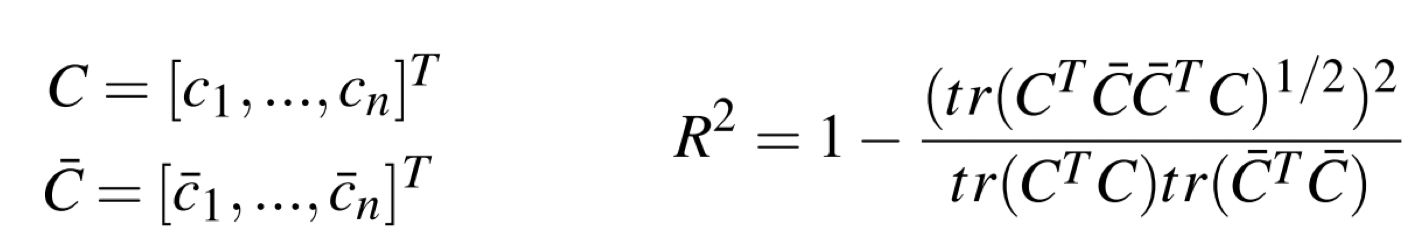
4. 实验
- 本文设计了三种不同的图数据:网格,星形,随机网络,使用 PivotMDS 和 ForceAtlas2 算法生成布局结果,并对于数据集进行了训练,验证,测试集的划分。总共有 30000 以上的数据行,每个数据在 20-50 点左右。
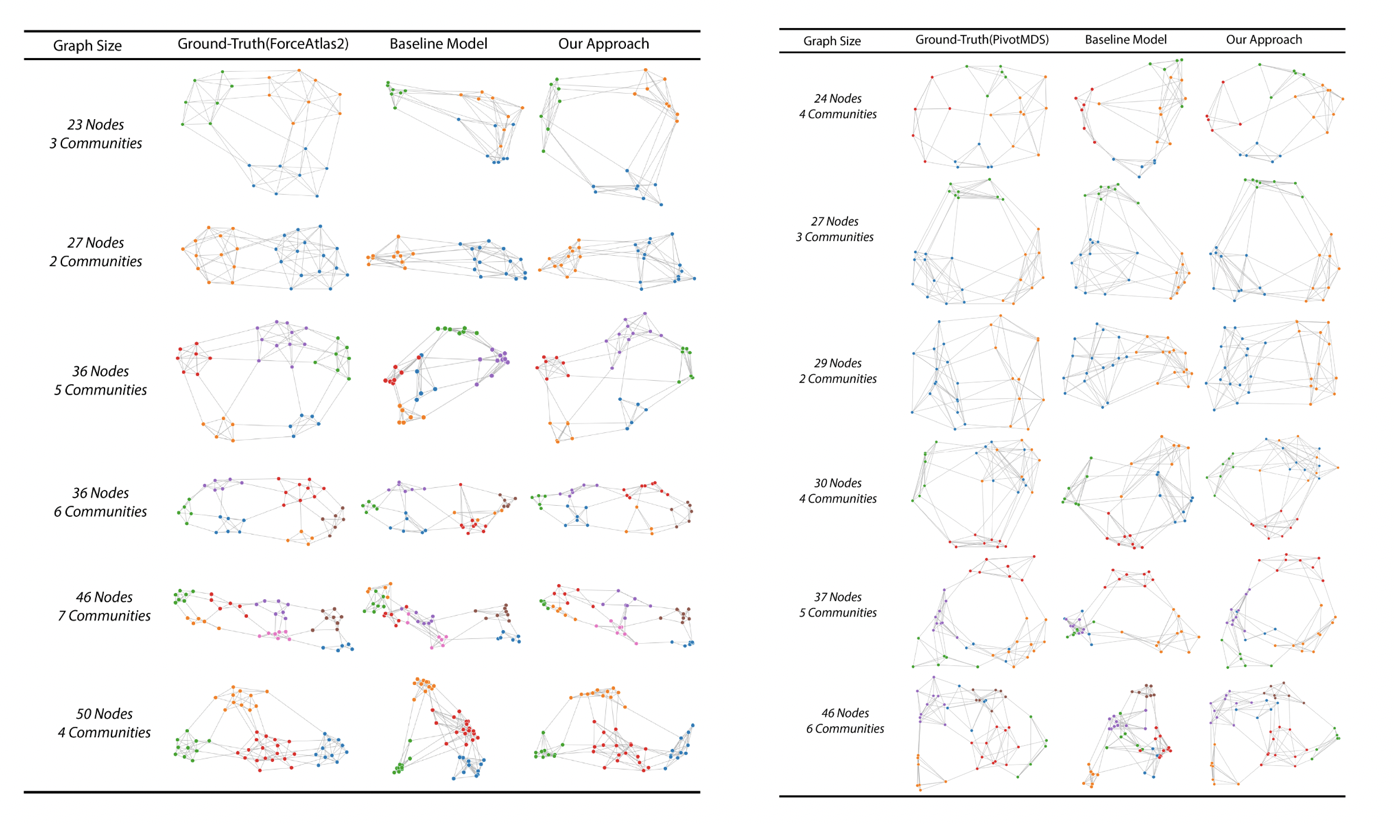
- 通过实验发现,双向 4 层 LSTM 具有较好的效果, 将其作为和本算法比较的 baseline。实验中,在三种数据集上分别训练 baseline 和 本文算法,将输入向量定为 35 的长度。其中随机网络的可视化如下所示。
- 本文还从 Prostats loss(模型 loss),边交叉($A{ec}$),点聚集($A{no}$),聚团覆盖($A_{co}$),运行时间这几个指标进行了评估,实验结果如下所示。左上模型 loss,右上运行时间,下面是剩余三种指标。

总结
本文从结构来看非常完整,工作量也很足。但还是有很多不足之处,比如:生成输入向量的算法依然不稳定,只在小数据(20-50 点)work,模型无法解释,学习不同的布局数据需要重新训练等问题。作者也提出了要把算法改进到大规模图数据上的设想,除此之外作者提出能否将方法应用到动态图当中。
✉️ cadhyz@zju.edu.cn