Graph Layouts by t-SNE

论文：Graph Layouts by t-SNE

作者：J. F. Kruiger, P. E. Rauber, R. M. Martins, A. Kerren, S. Kobourov, A. C. Telea

发表：EuroVis 2017

介绍

图布局是信息可视化中一个重要的任务。然而，随着数据量的增加，传统的图布局方法生成一个“好”的图布局结构越来越困难。降维方法可以将一个高维向量映射为低维空间中的向量，这和图布局的目标是类似的。尽管基于降维的图布局似乎很简单，但是这方面却少有相关的工作。这片文章基于对 t-SNE 降维方法提出了一个新的图布局方法，tsNET（）。tsNET（）将原始的图的拓扑结构表达为一个距离矩阵，并且通过对 t-SNE 目标函数的少许修改，达到更好的图布局结果。

背景

t-SNE 是目前最有效的可视化高维数据的降维算法之一。t-SNE 首先定义了输入空间和布局空间中选取一个点对的概率。其中输入空间一个点对的概率是基于它们之间欧式距离的高斯分布计算得到：

$p_{j | i}=\exp \left(-\frac{d_{i j}^{2}}{2 \sigma_{i}^{2}}\right) / \sum_{k \atop k \neq i} \exp \left(-\frac{d_{i k}^{2}}{2 \sigma_{i}^{2}}\right), \quad p_{i | i}=0$

布局空间中选取一个点对的概率是基于他们之间欧式距离的 t 分布计算得到：

$q_{i j}=q_{j i}=\frac{\left(1+\left\|\mathbf{y}_{i}-\mathbf{y}_{j}\right\|^{2}\right)^{-1}}{\sum_{k, l \atop k \neq l}\left(1+\left\|\mathbf{y}_{k}-\mathbf{y}_{l}\right\|^{2}\right)^{-1}}, \quad q_{i i}=0$

数据点在二维平面的坐标就可以通过最小化输入空间和布局空间中点对概率的 Kullback-Leibler 散度求得。

方法

给定一个图，tsNET 算法首先计算了节点之间最短路径长度，将其类比为 t-SNE 中高维向量之间的距离。然后，tsNET 采用了 t-SNE 的目标函数，并且增加了额外的两个惩罚项：

$C=\lambda_{K L} C_{K L}+\frac{\lambda_{c}}{2 N} \sum_{i}\left\|\mathbf{y}_{i}\right\|^{2}-\frac{\lambda_{r}}{2 N^{2}} \sum_{i, j \atop i \neq j} \log \left(\left\|\mathbf{y}_{i}-\mathbf{y}_{j}\right\|+\varepsilon_{r}\right)$

其中，第一项是原始的 t-SNE 的目标函数，第二项是压缩项，可以用来加速求解过程的收敛，第三项是为了防止数据点之间过于靠近，从而得到一个更理想的布局结果。如下图所示，简单地基于 t-SNE 并不能得到一个非常好的结果，这是由于 t-SNE 的目标函数是非凸的，优化过程很容易陷入到局部最优。因此，作者又提出了 tsNET*，将 Pivot MDS 的布局结果作为迭代初值，然后由上述目标函数继续优化，这样能够生成可读性更强的图布局结果。

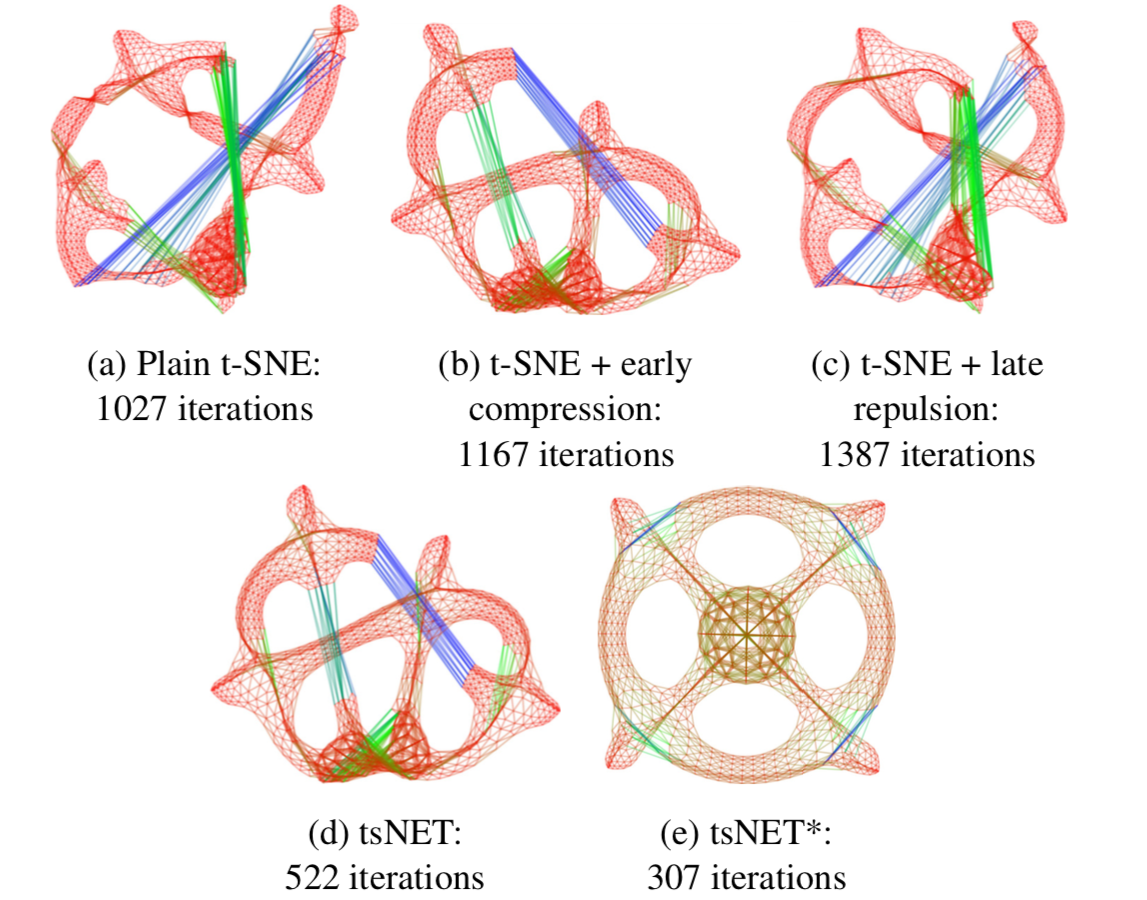
实验评估

Normalized stress metric.Normalized stress metric 是用来描述所有点对之间在图上距离和实际布局距离的误差。如下图所示，tsNET（*）取得了相对还可以的结果，虽然其他有些方法的 stress 更低，但是在后面可视化结果中我们可以看到，更低的 stress 并不意味着可读性更高的布局结果。

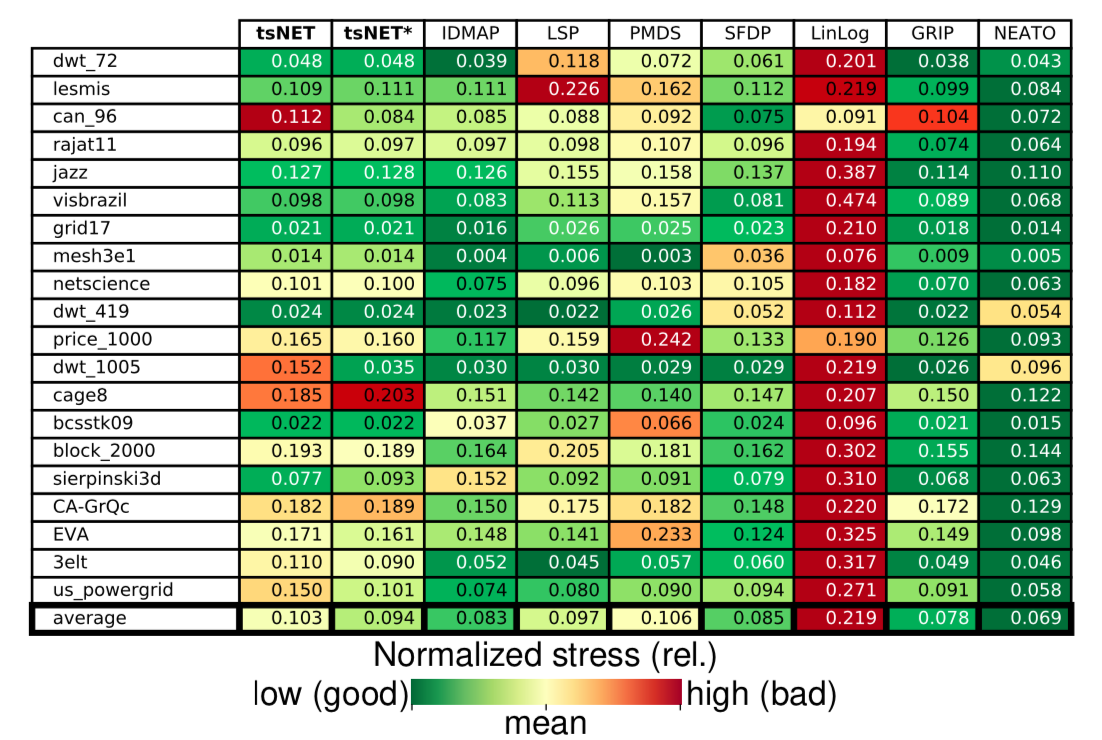
Neighborhood preservation metric. 相比于 stress 的度量方法，我们认为局部邻居的保持率更加重要：如果两个节点在图上是邻居，那么我们希望它们在布局空间中也是邻居。Neighborhood preservation metric 的计算方法是求得每个节点在图上最近邻集合与布局空间最近邻集合的 Jaccard 相似度。如下图所示，tsNET 在所有对比方法中取得了最优的成绩。

布局结果

多个方法在不同数据集上的图布局结果如下图所示，我们可以看到 tsNET*的布局结果更具有可读性。

总结

本文基于降维方法 t-SNE 提出了图布局算法 tsNET（）。tsNET（）在局部邻居的保持率上取得了最好的成绩，同时它的布局结果也更具有可读性。

Questions & Discussion： ✉️ minfeng_zhu@zju.edu.cn