Towards Unambiguous Edge Bundling: Investigating Confluent Drawings for Network Visualization
作者: Benjamin Bach, Nathalie Henry Riche, Christophe Hurter, Kim Marriott, Tim Dwyer
会议:TVCG2017
一、主要贡献
提供了一个普适的 CD 算法
通过调研生物、社交关系等方面的关于网络的文献,总结了一些网络中的主题图案, 并基于这些主题图案进行评估
评估可读性的用户调研
二、相关工作(边捆绑)
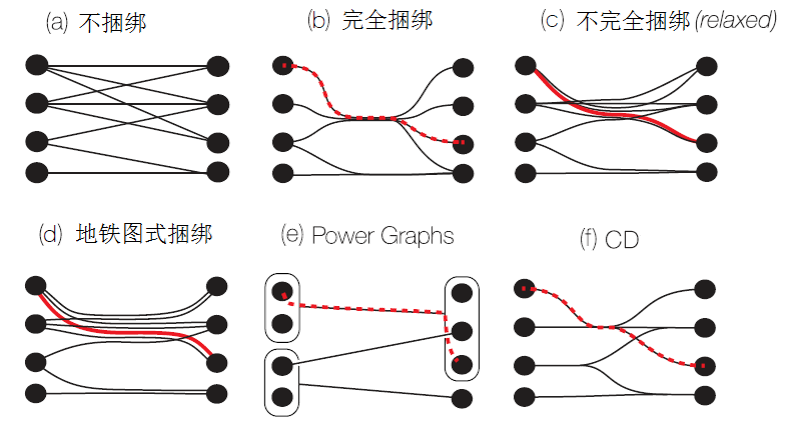
边捆绑是指在边密集的图中,为了节约空间,将空间上相近的边绑定到一起。这样做可以让图更加清晰,但是没有限制的边捆绑也会误导用户。比如说在图 b)中,用户可能以为左侧第二个点和右侧全部点都有连接关系,但是对比图 a)并不是这样。一种解决方式就是将捆绑放松(如图 c))。但是这样密集的边依然会让用户难以辨别。图 d)中的地铁式捆绑将捆绑的地方拆分开平行绘制,相对来说更清晰一点。图 e)的 power graph (PG)是将有相同连接关系的点用圈合并为一个组,通过一条连接到圈上边代替原有的很多条边。在基于 CD 的边绑定中,两条边只有确保一端的每一个点都和另一端的每一个点相连才会绑定到一起。遗憾的是这种方法之前一直局限于层次图和哈斯图的构造。而本片文章在方法上的贡献就是基于 PG 方法将 CD 拓展到任何一种图的边绑定上。
三、CD 方法
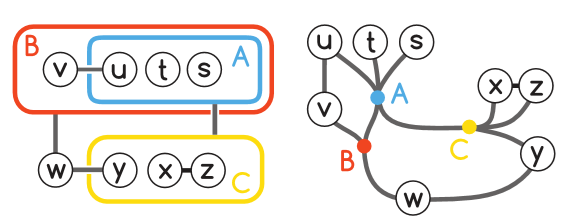
- 找到 PG 和 CD 的对应关系,通过 PG 构造 CD:
有共同邻点的组 → 生成一个 bundle 的链接点(routing node)
组内节点 → 连到相应链接点上的点
组包含 → 子组内的点通过子组的链接点再连到父组链接点上
组间边 → 链接点之间的边
- 绘制
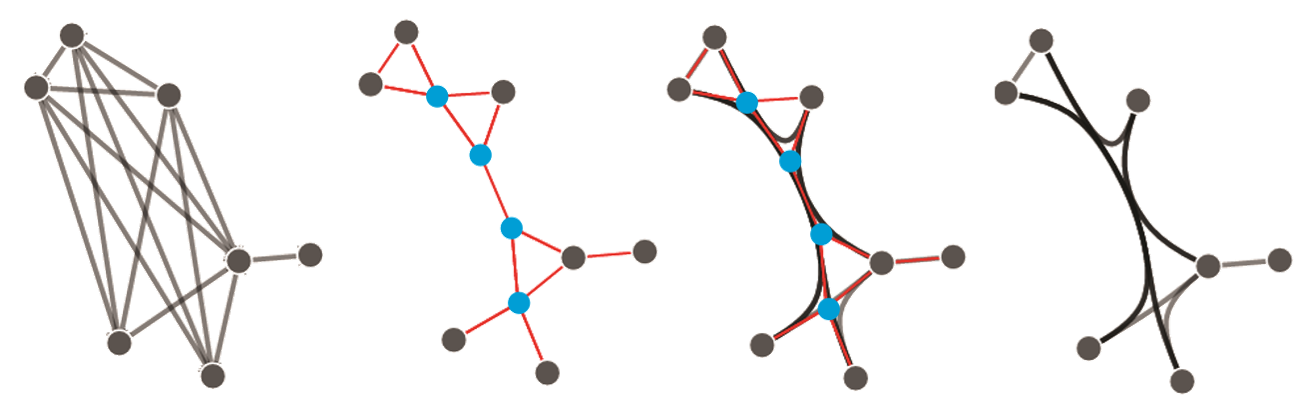
- 点布局:将图中点(灰色)和基于 PG 生成的链接点(蓝色)通过力引导等方法定位
- 边绘制:找到相连两点经过链接点连接的最短路径,作为控制点,用 B 样条方法绘制曲线
- 优化
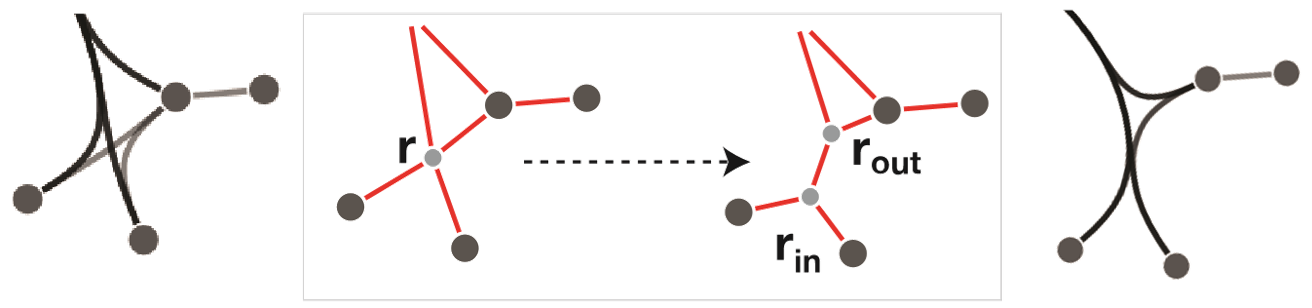
作者发现,当一个链接点的出度和入度都大于 1 时,结果会产生交叉。为了解决这个问题,作者巧妙地将链接点差分为入节点和出节点,基于它们绘制的 B 样条曲线不会出现交叉问题,而且可以完美地绑定到一起。
四、基于不同主题的评估
作者总结了高度相连的节点组、完全子图、星、关键节点等等。
其中,CD 方法比较擅长突出 n-partite components、星等图案。不过,在展现完全图的时候,由于 PG 算法的分组顺序不同,整张图看起来会有层次感,比较像大家认知中的树。
第一个代表了一对节点的临节点一致,且相连的情况。第二种就是上文提到的完全图,在这里有点像树状结构。最后是一些会有急转弯的线。当生成很多链接点,且它们不是单纯的包含关系时,就会出现一些急转弯。
五、用户调研
调研问题:初学者对低级任务的执行能力;和传统方法相比有什么优势;和原方法 PG 相比如何;用户有怎样的主观偏好。
对比技术:MG(地体图式绑定)、PG、EB(普通 edge bundling)、CD。
任务:给出起点和终点找最短路径。
实验过程:15 个初学者先对每个技术做 12 个练习,再分别对每个技术分别进行 18 个实验。
准确率分析:
通过 Friedman 非参数检验,整体结果是 PG(86%)没有明显优于 MB,但是有明显优于 CD(77%)和 EB(77%)。
作者提到在 CD 中用户会被边的 bundling 的曲率误导,忽视一些更短的路径。如果将任务改为找路径,那么 CD 方法的错误率可以从 23%下降到 8%。
- 用时分析:
这里只对找到正确答案的数据进行分析。作者分别使用了 RM-ANOVA 和 MLM 方法分别对重复测量中的被试内因素和随机效应进行了避免,得出了相似的结果,即 PG 优于 MG 和 CD 方法,EB 则是比较差。这是因为在使用 EB 的时候,用户需要花很长时间从绑定中辨别边的走向。
- 主观评价:
作者从信心、易学、清晰和整体四个方面对四种方法进行了 likert 五级问卷调研。
PG 方法虽然在之前的两项指标中都领先于别的方法,但是由于这个方法对于初学者来说是难以掌握的,大家对通过这个方法得出的结果信心不是很强。整体指标比较好的还是 CD 方法。
六、总结
CD 方法虽然解决了边绑定上的歧义,但是其构造方法比较复杂,随机分解可能导致一些误解,还有很大优化空间、
✉️ wangxumeng@zju.edu.cn