论文:A Visual Analytics Approach for Categorical Joint Distribution Reconstruction from Marginal Projections
作者:Cong Xie, Wen Zhong, and Klaus Mueller
发表:VAST 2016
介绍
通常情况下,我们获得的多变量数据并不是等多元元组的集合,而是一些属性的子集的投影。例如,我们可能会找到有 5 个属性的数据,但我们得到的并不是一个完整的表格,这些数据以两两维度存储在六个表中。所以我们想要从边缘分布重构联合分布。目前已知的方法都通过迭代过程来估计联合分布。当前的这些方法存在以下两个问题:一、没有足够的边际分布和专家知识,结果的误差较大。二、如果属性不是数值型的而是类别型的,求解过程中的正则化是不适用的。作者提出了一个结合多种数据和领域专家只是的可视分析方法,以迭代的方法来缩小合理解的数量。
方法
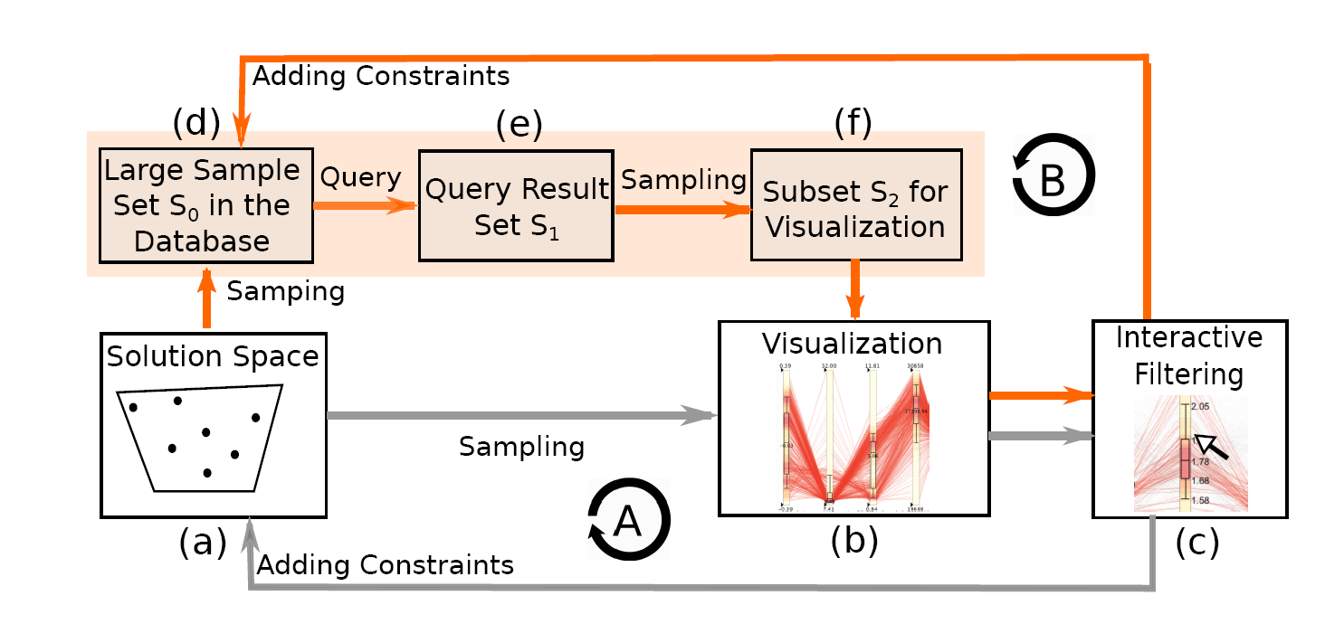
作者提出的用于重构联合分布的可视分析的方法主要包括如下几步:
重构并且缩小解空间:通过求解方程得到解空间 P,然后通过额外的约束比如领域知识来缩小解空间的范围
采样缩小的解空间:使用 Hit-and-Run 采样方法对解空间进行均匀采样
可视探索过滤解空间:从采样点中提取出一些列特征,并用平行坐标的方法可视化。用户可以探索过滤解空间
问题定义
给定 K 个属性, l 个边际概率, 需要估计每个元组 t={A_1=a_1,A_2=a_2, …,A_k=a_k}的联合概率。通过以下的公式可以利用边缘分布求解联合分布,其中 x 表示联合分布,y 表示边缘分布:

约束条件
由于解的空间维度太高,维度数随着属性数增加而指数增长,我们需要对解空间加入足够多的约束条件,降低解空间的维度,使得我们可以更好得逼近比较正确的解。
上界和下界约束:联合分布的值最小不会低于 0,最大不能超过对应的边缘分布的值。
领域知识:我们可以加入足够多的领域知识限制来缩小解空间的维度,这也是我们在交互式可视分析中可以添加的约束
2.1 协方差: 比如,无关属性间的协方差应该为零
2.2 变量范围:除了上下界,我们可以依照某些领域知识确定变量的范围,如,新生儿的男女比例在 1 左右
整数约束:由于有些数值必须是整数,我们可以过滤许多非整数的数值
定义解空间特征
由于解空间维度较高,导致平行坐标轴不能显示全部的维度或者降维算法太复杂导致维度难以理解,所以我们自己需要定义一些恰当的特征。这些特征要有足够的能力来帮助我们降低解空间的维度,它们需要有以下特征:
较高不确定性的变量:病人的数据库中,如果我们发现病人的年龄是均匀分布的,那么年龄这个维度需要重点研究。
一组变量的总和或者期望:早高峰的车辆是比较多,那么早上的同行时间期望值应该在早高峰附近
变量的比例或者协方差:人口的男女比例应该是接近 1 的
可视化设计
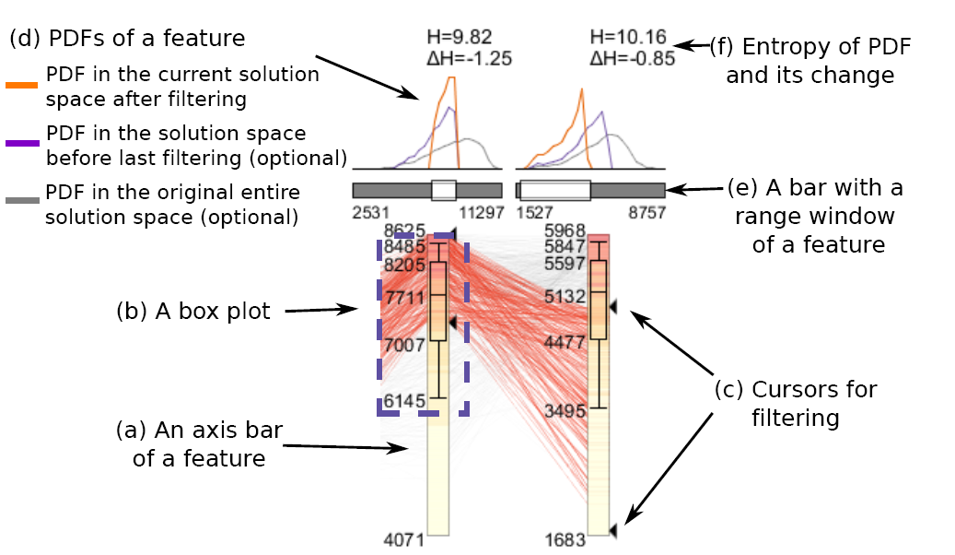
可视化设计主要是基于平行坐标图的改进,主要考虑了两点:特征的分布情况以及特征分布的变化图。对于特征分布,作者使用了盒须图展示了数据分布的中心点、四分卫点和 10%的位置,同时也使用了热力图来展示概率函数。对于特征筛选条件,系统提供了游标进行特征范围控制,用户可以滑动游标来给解空间增加约束条件。对于特征分布的变化,原始的概率分布由灰色曲线表示,过滤前的概率分布由紫色曲线表示,滑动游标后的概率分布由橙色曲线表示。
总结
作者提出了一种从多个边缘分布重构联合分布的可视化方法,这种方法可以将可视分析和算法的结合,将专家知识融合进系统中,对联合分布进行迭代式求解。
✉️ minfeng_zhu@zju.edu.cn