中文题目:多类散点图的可视简化与探索
作者:陈海东,陈为,梅鸿辉,刘致奇,周昆,陈伟锋,顾文涛,马匡六
发表会议:VAST2014
散点图(scatterplot)是一种使用非常广泛的可视化技术,常用于聚类分析、离群点分析、相关性分析等。多类散点图(multi-class scatterplot)作为散点图的一种扩展,其常用于比较分析应用。然而,随着数据规模的增大,有限的屏幕空间所造成的散点覆叠(overdraw)问题极大地限制了用户对可视化结果的正确感知。此外,不同的散点绘制顺序也会造成可视化结果的不一致性。如图 1 所示,不同的散点绘制顺序致使同一散点数据呈现出不同的可视化结果。
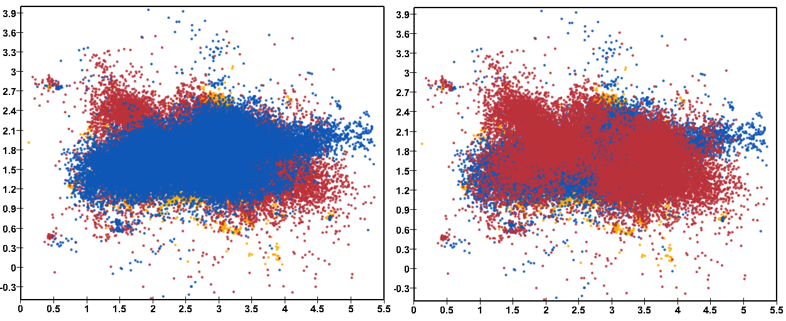
为了克服散点覆叠问题,可视化研究者们提出了一系列方法。改变散点的可视属性(如大小、透明度)是一种非常直观和简单的做法。然而,当散点的可视属性编码了其它信息时,该类方法易造成错误的理解。密度估计(density estimation)是另外一种可用于解决大规模散点数据的可视化方法。该方法易忽略低密度区域中的数据点。当应用到多类散点数据时,该方法还涉及多变量数据场的混合。这本身就是一大可视化难点。另外一类解决散点覆叠的方法称之为空间重分布(spatial redistribution)。其核心思想是将相互覆盖的点移至空白屏幕区域。这类方法本质上改变了数据的内在分布,可视化结果必然存在偏差。交互技术,如缩放(zooming)、焦点上下文(focus+context)亦可用于规避覆叠散点数据的探索。
本文提出了一种基于多类蓝噪声采样的方法实现多类散点数据的可视简化。为了增强简化结果的感知,本文还提出了一个散点颜色优化模型和一些散点形状设计方案。
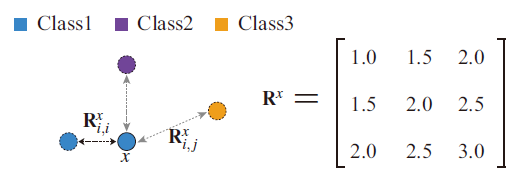
可视简化的基本目标是减少显示数据点的数目同时保持不同数据类之间的相对密度特征。为了达到这一基本目标,本文采用了魏立一等人最新提出的多类蓝噪声采样算法。该方法是单类蓝噪声采样算法的扩展。其采用了一个矩阵约束不同数据类采样点之间的最小距离。如图2 所示,该矩阵的对角线元素约束了同类采样点之间的最小距离,非对角线元素约束了不同类采样点之间的最小距离。
试验中发现,直接采样重构的连续密度场容易生成一些实际数据中不存在的数据点,如图3中图里红色矩形区域所示。为了避免该缺陷,本文选择在由输入多类散点数据组成的离散空间内进行采样。
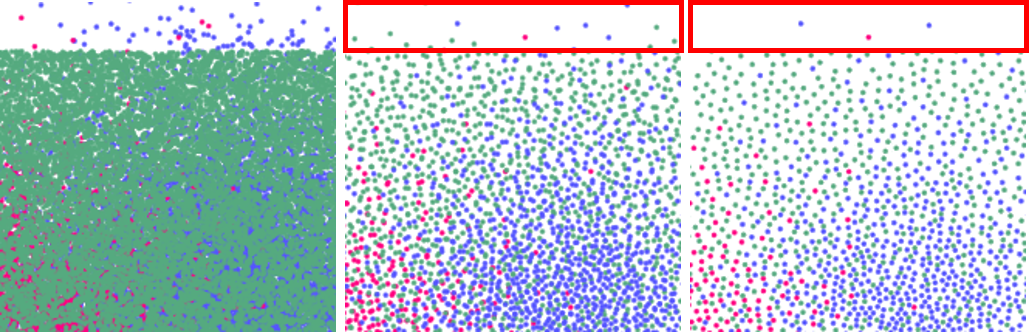
视图缩放操作中采样结果的一致性是另一个需要重点考虑的因素。每当视图进行缩放时便执行采样将不可避免的造成不同缩放比例下采样结果的不一致性问题。如图4所示,粗略层次的采样结果(如,红色区域中的洋红色数据点)并不是精细层次采样结果的子集。
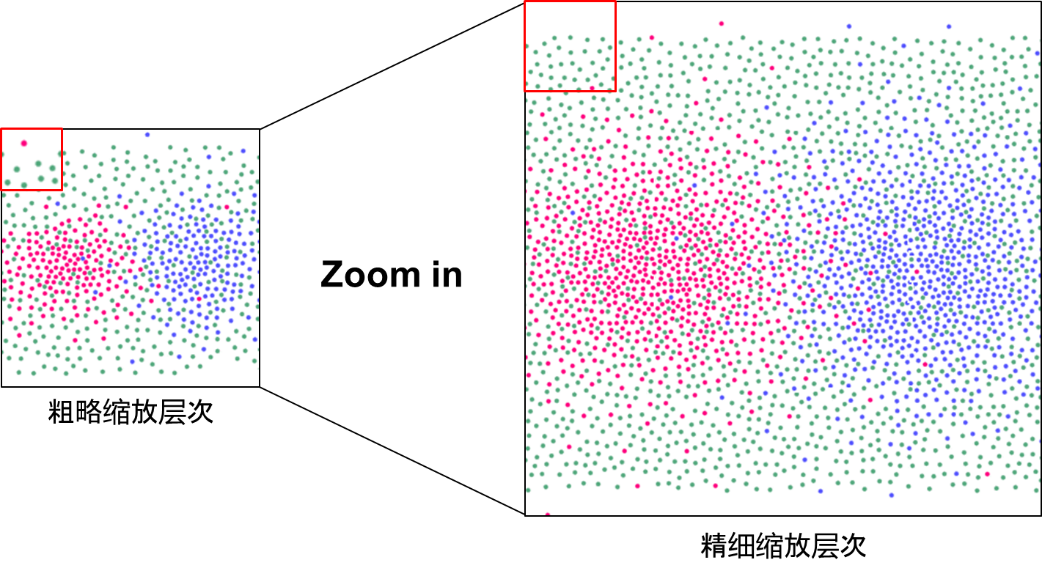
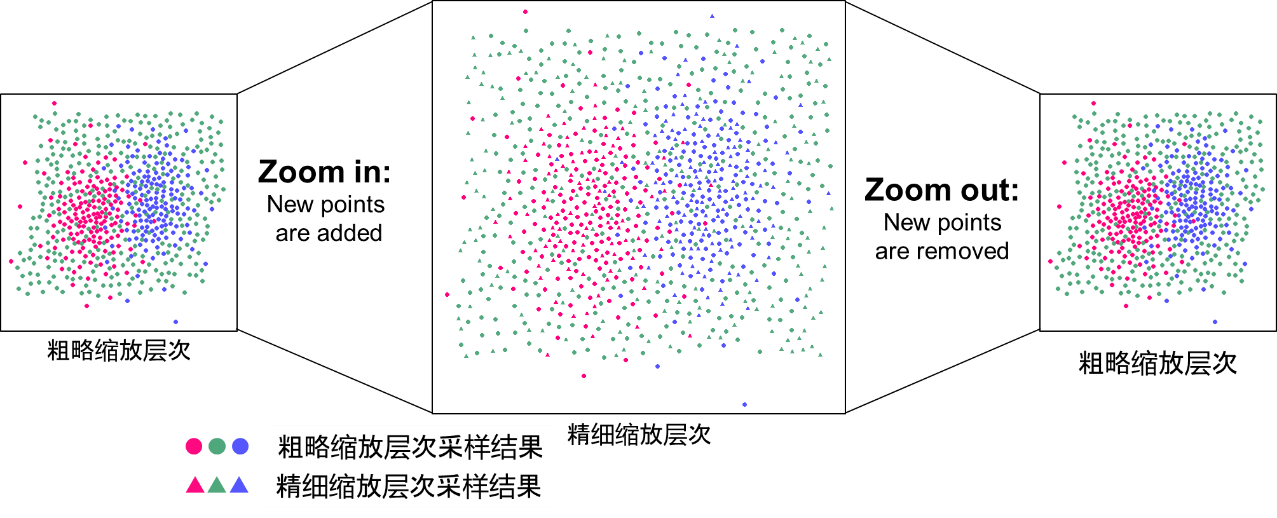
为了保证在视图缩放过程中采样结果的一致性,本文提出了一种层次化采样模式。其核心思想是在采样过程中将所有粗略层次的采样结果作为当前精细缩放层次采样时的约束。可视化时只需将当前缩放层次之前的所有采样结果绘制到视图中即可。通过这种处理方式,当视图放大时新的点将逐步加入到当前视图中,当视图缩小时新增的点将逐步地被移除当前视图。这种层次式地采样模式保证了采样结果在不同视图缩放层次之间的视觉一致性。如图5所示。
颜色是区分不同数据类的一个重要可视变量。未经优化的颜色设计将导致可视化结果中的重要特征无法被用户正确感知。本文通过求解以下优化问题在CIELab颜色空间中找到一组颜色集以保证不同数据类之间具有足够区分度。
其中,是颜色度区分度目标函数,约束了任意两个颜色在 CIELab 颜色空间中的最小感知距离。
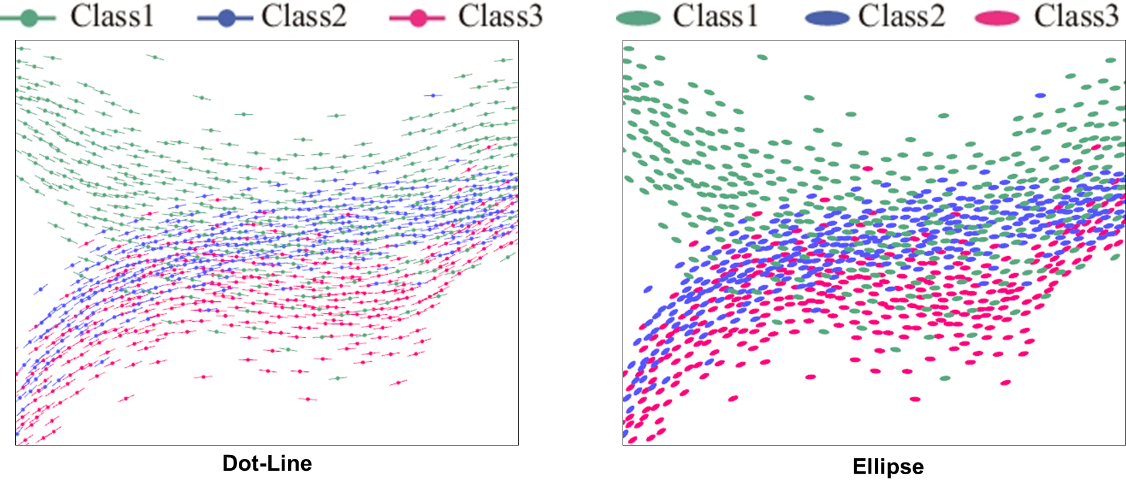
除基本的圆点表示外,本文还提供了两种散点形状设计以编码数据局部趋势信息,如图 6 所示。
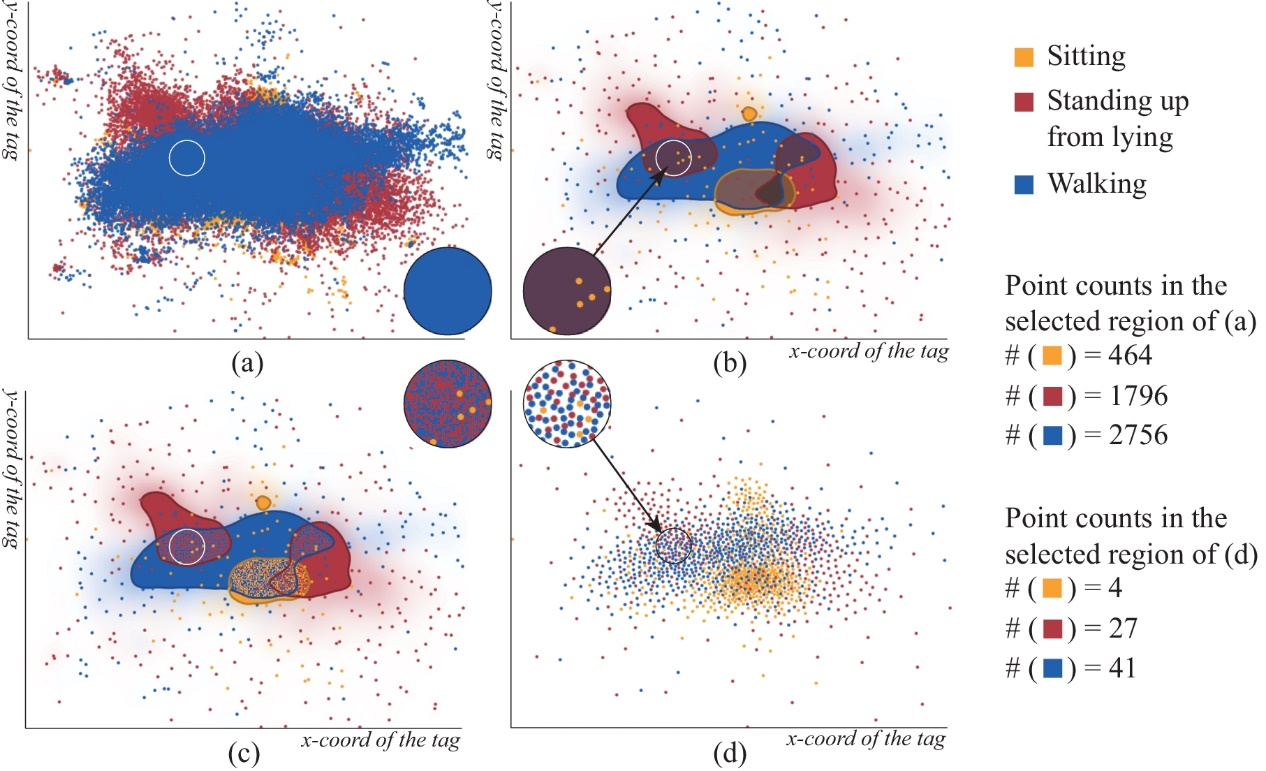
为了验证本文方法的有效性,本文对四种多类散点图可视化模式进行了对比分析,并进行了一项简单的用户研究。图7展示了这四种方法应用在一个数据集的结果。从结果中可以清晰的看出,传统方法产生了严重的散点覆叠问题。Mayorga等人提出的Splatterplot方法则会合成新的颜色,影响用户感知,如本例中所选区域所呈现的棕色。采用噪声扰动的方法可一定程度上避免该缺陷,增强用户对高密度重叠区域的区分度。本文的方法(如图7d所示)不仅规避了散点覆叠问题,还保持了局部区域的相对密度特征。
本文还将该方法应用到了两个实际数据中,图8展示了应用本文方法对NBA球队投篮数据进行简化的结果。从本文方法的结果中,用户可清晰的观察到,迈阿密热火更偏好于两侧底角三分,而孟菲斯灰熊队则更喜欢攻击篮下。
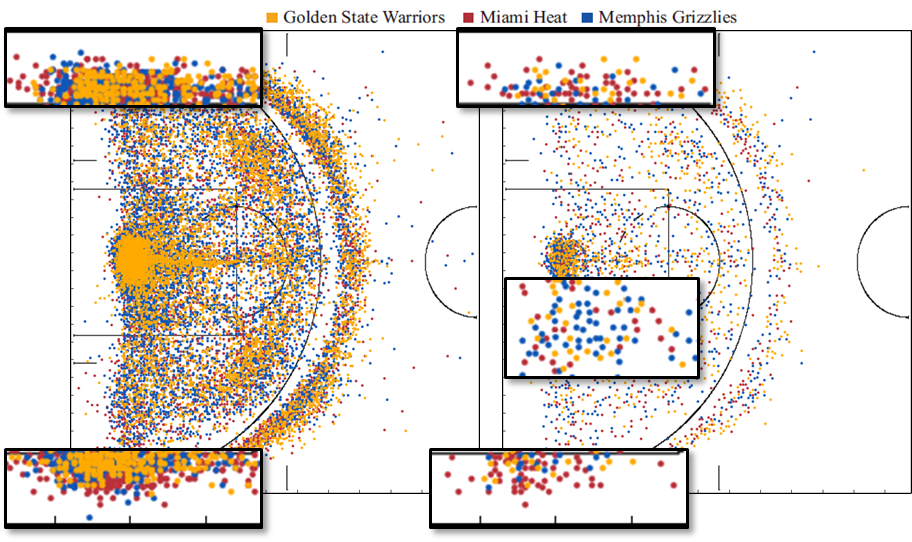
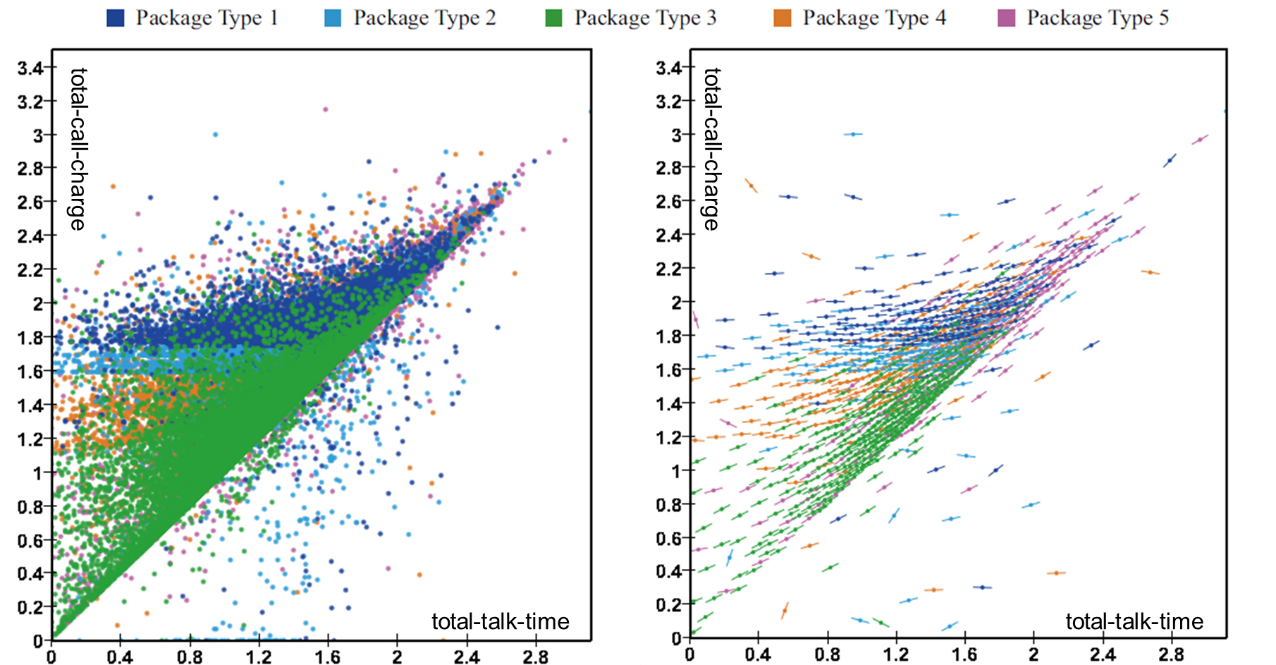
图9展示了本文方法应用于38万手机用户某月消费数据的可视化结果。从图9的右图可以清晰地看出不同套餐类型用户的消费行为特征。
结语:本文提出了一种新的多类散点图简化方法。该方法在规避散点覆叠问题的同时还保持了不同数据类之间的相对密度特征,是一种有效的定量分析方法。该方法的一个不足在于其亦忽略密度较低区域中数据的结构和特征。
Questions & Discussion:
✉️ zjuvis@cad.zju.edu.cn