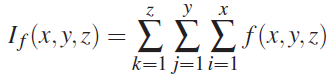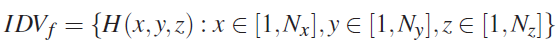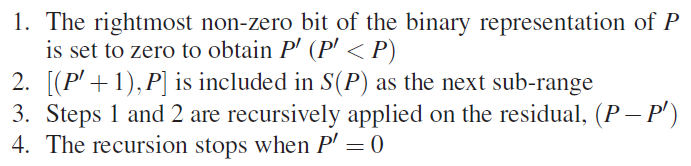作者 Abon Chaudhurl, Tzu-Hsuan Wei, Teng-Yok Lee, Han-Wei Shen
pvis2014 文章
区间分布查询是指对用户给定的一个 1D 或者 2D 或者 3D 区间,通常是 xyz 三个空间尺度内的大小(1D,2D,3D),返回区间内变量场的统计特性。例如,均值,标准差,熵等。
它的作用包括特征抽取,不确定性量化,数据压缩等。现存方法通常是对查询区间的变量场进行扫描计算,若查询区间大小或者相关参数发生变化,需要重新计算,时空负载过大,并且时空代价往往随着查询区间的尺度增加而增加。
针对上述问题,本文作者提出一个无视数据大小和查询区间大小的、常量应答时间的、低时空负载的区间分布查询框架。
作者通过引入并使用可预计算的、表达为直方图的积分分布(integral distribution)这样一种数据结构 降低空间负载;而在空间负载方面, 由于预计算的积分分布数据量较大,作者首先提出一套变换方法,将数据变得易压缩;然后将数据分解并建立索引;再用合适的压缩方法压缩。
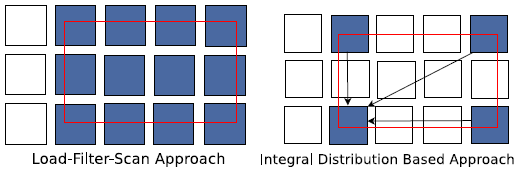
图 1
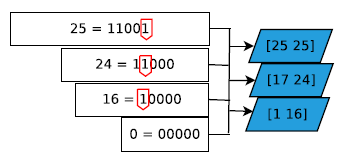
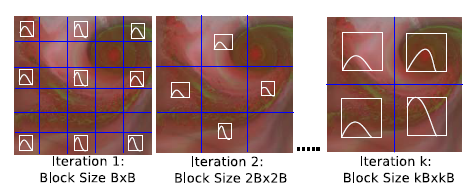
如图 1 左图所示,矩形为块状待查询区域(当数据尺寸很大时,亦可认为是一个数据文件),红框表示选中的查询区域大小,在用传统方法进行区间查询时,改变查询区间的大小即意味着重新计算区间内所有待计算的块,时空消耗显而易见。
本文方法如图 1 右图所示,无论查询区间大小以及原始体数据大小,只需要返回查询区间角点的值即可,1D 为 2 个点,2D 为 4 个点,3D 为 8 个点。每个点上都保存着从原点开始到该点的预计算后保存的计算量。由此可知,该查询的反馈是常量时间的。
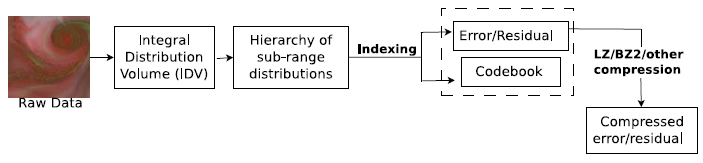
本文的主要思路如图 2 所示
首先将原始数据预计算,表达为 IDV;同时,为了加速计算,减少存储空间,将其分解为一些可重用的小区间分布进行表达。;其次,构建索引码表,为了提高解码的正确性,作者定义了两种变换方法,使得码表可扩充;然后,可使用无损压缩方法对码表进行压缩;最后交互地检索和重构区间分布。
下面是本文方法的详细过程.
上式是 Integral Volume 的表达式,f 表示标量场,该式意味着从原点到当前点的属性值累加。其表达式表明 任意区间的计算结果都可以通过其他子区间计算结果做加减法得到。
IDV 则代表 Integral Distribution Volume ,与 IV 相比,IV 计算的是数据值,IDV 则计算原点到 xyz 的统计直方图。
有了上述概念后,作者提出如下算法将整个 IDV 分解为很多个可重用的子区间数据块
算法包含 4 步,以 1D 的 P=16 查询区间为例,构建子块的过程如图所示。当 p 是 2D 或者 3D 的点时,先在每个空间方向上独立进行分解,然后合并,例如 p =(5,4),可以分为 x 方向 px=5 和 y 方向 py=4 两个区间独立进行分解,然后合并。
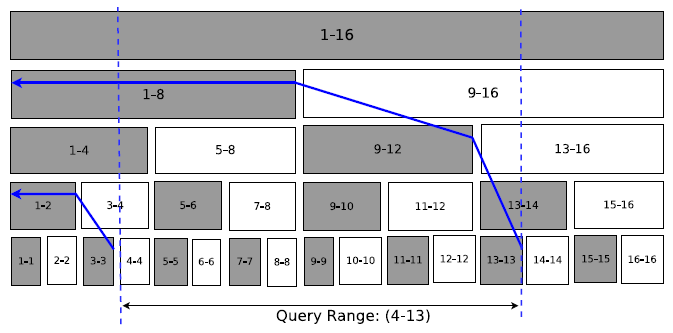
最终构建的树状层次性子块结构如下图所示
对于区间 4-13 的查询可由 p= 13 – p=4 得到,在图中的表示即是两条蓝色箭头所通过的块,查询结果作差即可。
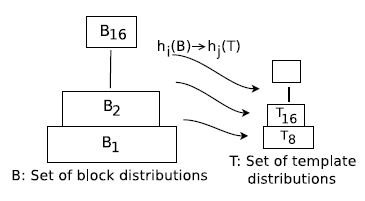
构建完该树状结构以后,作者使用下采样的原始数据构建索引码表,此处的思路类似向量量化,算法如下图所示
大小相同的子块(以包含的体素个数计量)被归为一类,逐类进行码表构建,示意图如下 top 图所示,实例展示如下 bottom 图所,读者可联系算法过程更好地理解实例展示的构建过程,B16 代表大小为 16 个体素的子块,对应 T16 代表大小为 16 个体素的码表元素。
构建完码表后,需要对码表和体数据的子块建立映射关系。映射的目标为 从码表中找到最好的近似去构建一个子区间。其所存在的最大困难为 码表大小(码表元素个数)远小于子区间的个数,很难为每一个子区间找到很好的近似 码表元素。于是作者提出两个变换算法,用以对码表进行变换,实质是允许扩展码表 。两种变换算法为 circular shift 以及 reflection,实质为对码表元素空间进行循环平移或者镜像映射,试图在该码表元素的变换空间中找到更好的码表元素以重构原始子块。在具体的 实现中会有加速算法,在一个缩小的、限定的空间进行变换和搜索,示意图如下
流程的最后一步即是对分割好的子区间,按照索引码表中的元素以及其对应的变换算法和残差进行解码重构,该步骤的算法流程如下
前述构建树状层次子块结构时,已经可以看出很多子块大小为 1,例如(4,4),这些块对最终的重构子块精度贡献不高,但是却占用同样的查询反馈时间。因此,可设置区间抛弃阈值 T,丢弃小的子区间,提高访问速度,减少存储空间。因为小的子区间贡献值小。T = 0 表示无损重构;T>0 表示近似重构。例如,h(65)可以分割为(1,64)和(65,65)后者可以被丢弃。
本方法的应用范围主要为,对三维空间中任意区间的某种属性感兴趣,并希望在动态变化计算域和查询域时,任然获得极高的时空效率,这种应用皆可使用本文的方法。下面举两个实例,第一个是局部统计分析,该应用通常以块或者体素领域为计算单位,块或者领域大小随着用户需求可动态变化。结果图如下
第一行的图表示飓风压力场均值的计算和查询结果,截断阈值分别为 0,32 和 64,第二行分别对应三种截断阈值下的性能分析。
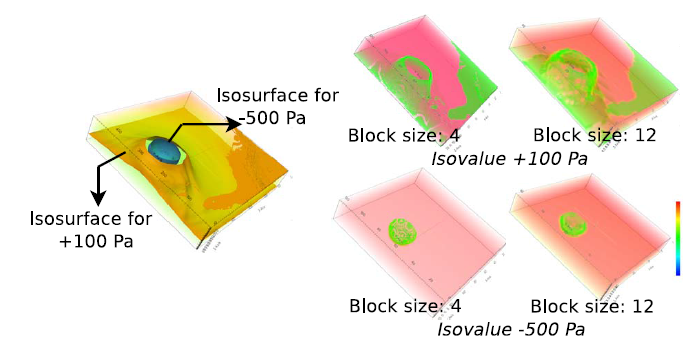
第二个应用为使用模糊等值面的特征检测,通常以块为计算单位,在对原始体数据没有有效认知的情况下,可以由用户给定一个 isovalue, 对每个块计算一个 likelihood value(统计分布),若该统计分布结果接近给定值,则认为该块或者领域包含 isovalue,即为等值面所在区域。一个应用实例结果如下图
本文详细的性能分析(sapce saving 等)可参考论文,作者希望在未来,可以把该项工作扩展到多变量数据;支持任意形状的区间查询(目前只支持沿 xyz 坐标轴的规则区间);实现一个 GPU 版本。
✉️ zjuvis@cad.zju.edu.cn