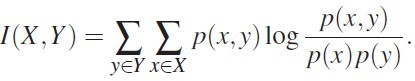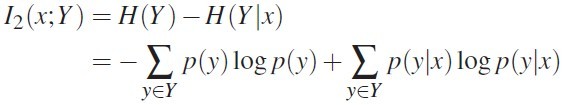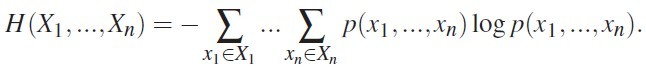文章:An Information-Aware Framework for Exploring Multivariate Data Sets
来源:SciVis2013
作者:Ayan Biswas, Soumya Dutta, Han-Wei Shen, Jonathan Woodring
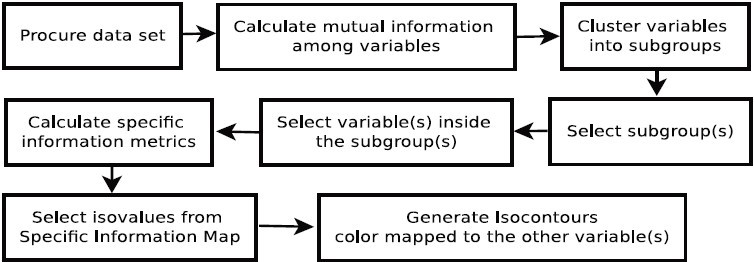
本文主要介绍了一种基于信息论的多变量数据可视分析框架构建方法,流程如图 1 所示
图 1
本文的目标是帮助用户探索多变量数据,确定重要区域或者用户感兴趣的区域 。依照流水线,在获取到数据集后 ,首先计算变量之间的互信息 ;然后基于互信息,将变量进行分类;再通过联合熵的值,选择一些类进行分析 ;在选取的类内部,通过变量的条件熵选取信息量最大的变量 ;选取变量后,计算具体的信息度量;最后通过计算和分析得到的具体信息度量图,选取变量的值,绘制等值面,进行可视化。
与本文密切相关的工作主要集中在三个方面。
- 信息理论及其在图形学和可视化方面的应用
- 多变量数据分析和平行坐标
- 显著性等值面选取
本文算法的主要步骤,可归结为 4 个。首先是介绍和定义多变量数据的信息重合。下面是几个重要概念的介绍和定义:
互信息(mutual information):两个变量之间的互信息表示一个变量相对于另外一个变量的信息量大小,比起相关性度量(correlation metric),好处是可以度量非线性关系 ,公式如图 2 所示
图 2
具体信息(Specific information): 变量 X 的一个特值 x,相对于变量 Y 的信息量大小; 其中 X 称为参考变量(reference variable)
具体信息的度量(I1 & I2): Surprise 和 Predictability,计算公式分别如图 3 和图 4 所示
图 3 图 4
本文使用参考变量的 specific information 确定显著性等值面;
显著性的计算定义如下:确定参考变量的一个特值后,另一个变量的不确定性减少的量的大小
I1,是指以 X 为参考变量,当 X 取 x 值时,Y 取 y 值的可能性的大小, I1 越大,这种可能性就越大;而使得 I1 越大的 x 的取值,即是我们在可视化中感兴趣的 isovalue
I2 表示给定 x 的取值后,Y 的不确定性的减少的量。
使得 I2 很高或者很低的 x 的取值,都是在可视化中很重要的量,因为意味着这些区域处于某种边界上。
假设有一个体数据,包含两个属性 X,Y;选取好参考变量 X 后,计算 I1 和 I2,首先,选取使得 I1 值很大的 X 变量值,设为 surprise ones,然后再判断他们的 predictability 值,如果 I2 值也很高,说明这些 X 的变量值对应的 isovalue 可表示另外一个变量(Y)处于稳定状态;否则,说明另一个变量处于变化剧烈状态。
计算出变量对之间的互信息后,为了使本文在 I-metric 下工作的更好,需要使互信息更大的变量对(即关联更紧密)聚集到一起,被归为一类,再选取其中包含最大信息量的属性作为参考变量。
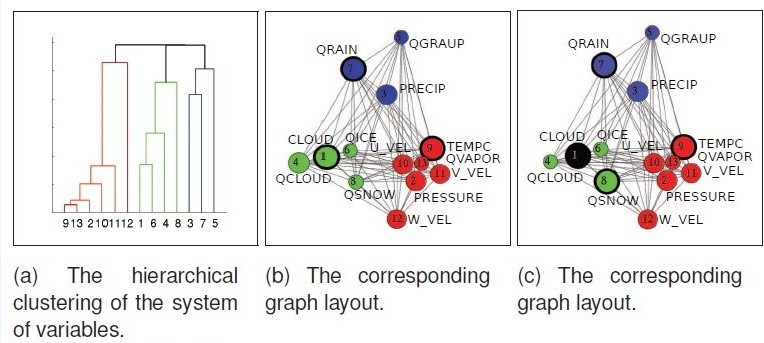
因此,按互信息的值自底向上对其进行层次性的分类,得到 K 个 group,再对分好的类进行力引导图布局,如图 5 所示
图 5
a 图视层次性的分类结果,b 和 c 是分好类后的力引导布局,12 个属性被分成 3 个类,分别用红绿蓝表示,每个点表示一个属性,线表示属性之间的互信息,互信息越大,距离越近,反之越远。
点的大小代表该属性的信息熵的大小,意味着信息量的大小。b 图中黑色边框包围的节点为系统第一次生成力引导图后推荐用户分析的第一个属性,每一次选取以后,其他属性的不确定性会发生变化,从而,必须
更新力引导布局,如 c 图,黑色的节点代表已经选中被分析的节点,黑色边框会自动转移到当前布局中下一个被推荐的节点。对于这一过程,如图 6 所示
图 6
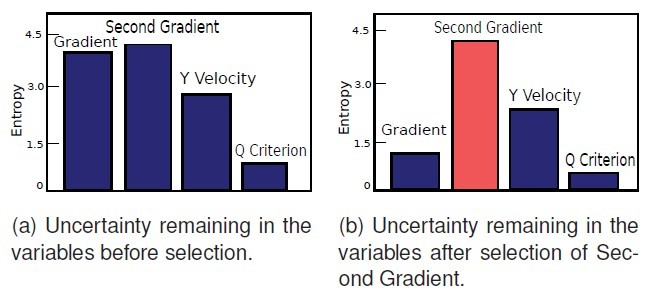
假设系统第一次生成布局后,一个 group 里属性的信息熵大小如图 6a 所示,依据信息熵,用户被推荐选择 second gradient,其次是 gradient,y velocity 和 q criterion。此时,代表 second gradient
的节点就会被黑框选中,当用户选择它进行分析后,力引导布局会进行更新,由于属性之间的相互影响和互信息的存在,一个变量的选择会影响其他变量的不确定性,也就是信息熵,因此,更新完以后的布局使得 Y velocity
成为下一个被推荐的属性节点。深入到信息论层面,这是由于单个属性的不确定新可以用信息熵表示,而多变量数据则对应的用联合信息熵表示其不确定性和信息量的大小,如图 7
图 7
而当我们选取(即确定)其中一些属性后,其他属性的不确定性变化,可用条件信息熵来表示,如图 8 表示 n 个变量,m 个已知的情况下,剩余的不确定性大小
图 8
有了上述理解之后,我们可以看一下文章所述框架的最终面目了。
如图 9 所示
图 9
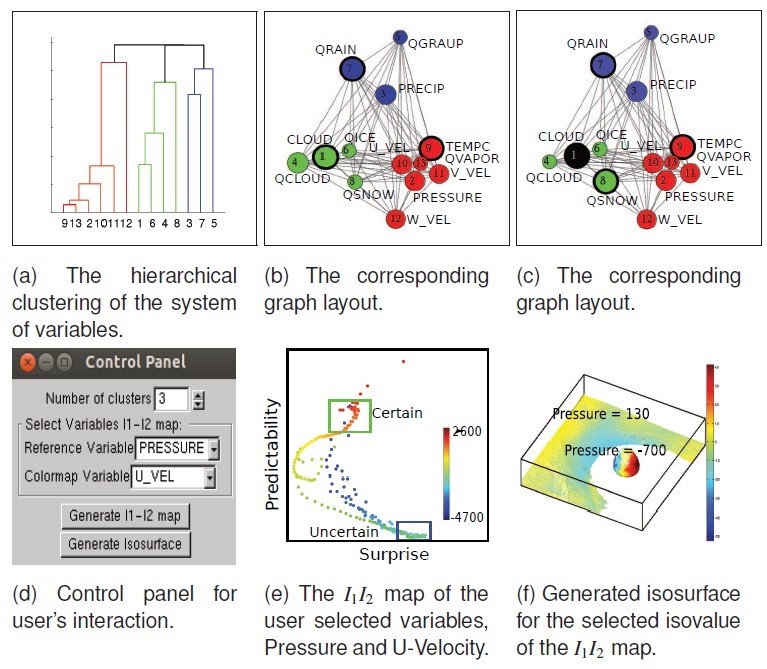
首先,我们队多变量数据计算互信息,依据该计算结果对属性进行分类,如图 9a,计算每个属性的信息熵,生成力引导布局,给出推荐属性,如图 9b,用户选取属性后,更新布局。
同时,对用户选取的属性,在如图 9d 所示的界面中设置好属性对,参考变量等,然后计算其 I1 和 I2 值,获得如图 9e 所示的结果,再依据 I1 和 I2 值的大小组合确定感兴趣区域,用框选取,该处对应的参考变量值即被作为
等值面值,在空间域中进行等值面绘制,帮助用户观察分析结果,如图 9f。
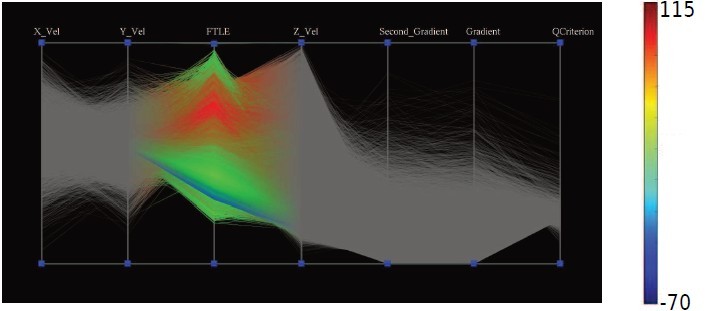
除了上述空间域的观察和探索方式,本文还提供了数据域的观察方式,使用平行坐标展现一个类中属性的关系。如图 10
图 10
此处,颜色编码的是 I1 和 I2 的比值(直接代表不确定性大小)或者 I1 和 I2 的乘积(直接代表确定性的大小)
本文给出三个数据应用实例,分析流程和图 9 基本一致,此处不赘述。
此外,作者还邀请了 Los Alamos National Lab 的一些科学家进行了 User evaluation。对于科学家们的改进建议,总结如下:
- 加入一些其他分析工具,如散点图矩阵
- 时间域操作、分析 。
- 力引导图可选择去除边(视觉遮挡)
- 专家先验知识的变量组合与基于信息论得出的组合不一致,他们依然渴望探索这种先验知识所已有的变量组合。比如,盐度和气压的关系可能是科学家在先验知识中认为结合比较紧密,比较有探索意义的属性对,而实际由信息论得出的分类结果不支持这种对比和分析,此时无法满足专家期待和要求。
最后,本文的主要计算时间集中在 I1 和 I2 的计算上。
✉️ zjuvis@cad.zju.edu.cn